Simulation de la rupture des composites
Simulation numérique du comportement et de la rupture des solides composites ou homogènes
Numerical simulation of the mechanical behaviour and fracture of composite or homogeneous materials
Méc. Ind. et Matériaux, Vol. 48, n° 3, 1995
B. SCHAEFFER
RÉSUMÉ
Deform2D est un logiciel de calcul par différences finies, entièrement non-linéaire fonctionnant sur un microordinateur Macintosh, mettant à profit son interface utilisateur. Le maillage est automatique par un simple clic dans un contour. Le logiciel est particulièrement adapté à la simulation des chocs, mais des essais quasi-statiques peuvent aussi être simulés. On a pu visualiser la propagation des ondes, des bandes de glissement et des fissures. Les matériaux composites sont modélisés en répartissant les deux composants dans différentes mailles selon une structure régulière décrite par un motif graphique.
MOTS CLÉS
Différences finies - Dynamique - Matériau composite - Logiciel - Rupture - Simulation numérique.
ABSTRACT
Deform 2D is a fully non-linear bidimensional software working on a Macintosh microcomputer, taking advantage of the graphic user interface. Automatic meshing is performed with a simple click in a contour. The software is especially adapted to the study of impacts but quasi-static tests may also be simulated. Propagation of waves, glide bands and cracks has been visualized. Composite materials are modelled by distributing two component materials over the meshes according to a periodic structure described by a graphic pattern.
KEY WORDS
Finite differences - Dynamics - Composite material - Software - Fracture - Numerical simulation.
1. INTRODUCTION
La simulation numérique du comportement dynamique des structures existe depuis plus de vingt ans, mais elle nécessitait des moyens importants. Avec l'avènement des microordinateurs, les expériences numériques deviennent possibles en laboratoire. Le coût des calculs devient faible et on peut partir directement des équations de base sans avoir à les intégrer partiellement dans le but d’accélérer les calculs.
Le procédé de calcul [1] consiste à découper le milieu déformable en quadrilatères où les variables (variables d’état et constantes du matériau) sont uniformes. La géométrie du problème est alors très simplifiée. Il n’est plus nécessaire d’homogénéiser et de faire appel à la théorie des corps orthotropes. Le coût du calcul sur microordinateur devenant inférieur à celui de la matière grise, on peut pousser jusqu’au bout la logique du tout numérique.
2. METHODE DE CALCUL
2.1. Déformations
La configuration d'un corps solide est décrite par un modèle mathématique continu dont les points géométriques s'identifient à la position des particules matérielles [2]. Un vecteur infinitésimal de longueur ds et de coordonnées dxi, devient, après déformation, un vecteur de longueur ds' et de coordonnées dx'i. Au second ordre près, les nouvelles coordonnées sont fonctions linéaires des anciennes, avec, comme coefficients, les gradients de déformation, ∂xi / ∂xj [3]. Les déformations εij sont données par:
![]()
est la déformation de Green. En appliquant la formule à une traction simple, on trouve [4]:
![]()
La déformation volumique est approximée par:
![]()
2.2. Contraintes
La loi de comportement ou équation d'état rhéologique [5] exprime la relation entre les contraintes et les déformations. On utilise ici les contraintes vraies ou euleriennes ou de Cauchy, relatives à la configuration déformée, et non les contraintes nominales (se rapportant à la configuration initiale).
Les composantes du tenseur des contraintes sont constituées d'une partie sphérique, correspondant à la pression, et d'une partie déviateur, correspondant aux cisaillements:![]()
La loi de comportement est séparée en une partie sphérique qui relie la pression au volume, et une partie déviateur. On a choisi une combinaison linéaire d'un solide hypoélastique et d'un fluide visqueux, c'est-à-dire un solide de Kelvin compressible, en incrémental:
Ce modèle rend compte de l'amortissement mais ne permet pas de simuler la relaxation des contraintes à allongement imposé. La loi de comportement est complétée par des critères de plasticité (Tresca) et de rupture (Tresca-Coulomb). Le second se distingue du premier par une variation linéaire avec la pression du cisaillement maximal.
2.3. Mouvement
Le mouvement d'un corps déformable se fait sous l'action des conditions initiales, et des conditions aux limites, selon les équations de la mécanique. Sous sa forme intégrale, la loi fondamentale de la dynamique, pour un élément de volume Ω, limité par une surface Σ, s'écrit:
où les Γi sont les composantes de l'accélération, les gi celles de la pesanteur et les nj celles de la normale à Σ. dV et dS sont des éléments de volume et de surface.
Si le domaine Ω est petit, la densité y est constante et les composantes de l'accélération vont s'écrire:
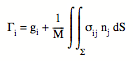
où
est la masse, constante, de l'élément de volume Ω. La connaissance des variables du membre de droite de cette équation permet de calculer le mouvement du centre de gravité du domaine Ω par une double quadrature, qui donne les composantes de la vitesse, puis les coordonnées.
2.4. Résolution numérique
Le milieu continu est découpé selon une grille (figure 1). La plupart des mailles sont des carrés sauf sur les contour où ce sont des quadrilatères. quelconques où les contraintes, les déformations et le matériau sont uniformes. On peut associer à chaque quadrilatère un triangle de référence, construit sur les diagonales, qui définit les déformations εij :
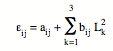
Les déformations sont donc une fonction linéaire des carrés des longueurs Lk des côtés du triangle de référence. La partie sphérique du tenseur des déformations est directement proportionnelle à la variation de volume, c'est-à-dire à l'aire de la maille (déformation plane).
Les conditions initiales et aux limites sont appliquées soit à des mailles (pression), soit à des noeuds (vitesse, position…) ou en effectuant des tests sur l'appartenance ou non d'un noeud à une région (contact) grâce aux fonctions graphiques du Macintosh.
Les contraintes sont évaluées à partir des déformations par l'équation d'état rhéologique (6). Le mouvement d'un noeud, considéré comme un point matériel confondu avec le centre de gravité de l’élément, est calculé en appliquant la loi fondamentale de la dynamique au quadrilatère, constitué de quatre demi-mailles, obtenu en joignant les quatre noeuds entourant le noeud considéré (figure 1). L'effort résultant agissant sur ce quadrilatère est la somme des forces surfaciques appliquées aux quatre diagonales entourant le noeud. On en déduit l'accélération puis les nouvelles coordonnées des noeuds.
Maillage d’une éprouvette de traction. Mesh model of a tensile specimen.
On doit respecter la condition de Courant-Friedrichs-Lewy [6] pour un calcul stable: la propagation des ondes durant un pas de temps ∆t doit être inférieure à la plus petite dimension de la maille. A cause de cette condition la durée d'un calcul est proportionnelle à la durée physique du phénomène simulé, d'où la nécessité d'effectuer les calculs à une vitesse de déformation aussi élevée que possible.
2.5. Interface utilisateur
Les contours définissant la géométrie du problème peuvent être dessinés avec la souris ou à l'aide des logiciels de dessin disponibles sur Macintosh, comme MacPaint ou MacDraw. La fenêtre graphique sert à définir la géométrie du problème par les contours à l'intérieur desquels on clique avec la souris après les avoir éventuellement modifiés pour être analysés par le logiciel.
Seule la pièce à déformer fait l'objet d'un maillage automatique. Il n'est pas nécessaire de définir les noeuds individuellement, même sur le contour, il suffit d'indiquer le nombre total de noeuds souhaité. Les contours sont de plusieurs
types: le domaine physique, la pièce mobile qui impose le déplacement, la zone sous pression, la pièce à déformer qui peut être multiplement connexe, éventuellement la partie de la pièce constituée d'un second matériau ou en matériau composite avec une structure choisie dans une fenêtre.
Le logiciel attribue à chaque maille les caractéristiques du matériau dont elle est constituée (deux matériaux au maximum), ainsi que les autres valeurs initiales et vérifie les conditions aux limites.
Fenêtres de dialogue de saisie des données numériques.
Dialog windows for numerical data input.
Les données numériques sont saisies dans deux fenêtres de dialogue.
On peut visualiser les contraintes, les déformations, les vitesses, etc et récupérer l'image calculée dans la plupart des logiciels Macintosh. La programmation est en langage Pascal Objet (MacApp). Un calcul de 5000 noeuds dure une journée sur Macintosh II.
3. APPLICATIONS
Les matériaux composites sont des matériaux inhomogènes par définition. Ils sont anisotropes lorsque les composants, même isotropes, ont une répartition anisotrope. L’homogénéisation nécessite l’utilisation des théories des corps orthotropes. On détermine expérimentalement ou à l’aide de théories micromécaniques leurs lois de comportement.
Une autre approche, celle qui est proposée ici consiste à partir directement des caractéristiques mécaniques des composants de base et à diviser le composite en mailles élémentaires où chaque maille (homogène et isotrope) est constituée d’un parmi deux matériaux constitutifs. A l’aide de motifs graphiques, on associe à chaque maille un pixel de façon à modéliser la structure du matériau composite. Un pixel noir correspond au renfort et un pixel blanc à la matrice. Il y a correspondance quantitative entre la composition volumique et la densité des pixels, sauf au voisinage du contour où les mailles ne sont plus carrées mais peuvent être des quadrilatères quelconques.
Ce modèle, très proche du réseau carré à deux constituants homogènes [7] est entièrement numérique et n’utilise pas d’homogénéisation analytique. Son inconvénient est de ne pouvoir faire varier les structures de façon continue à cause de sa nature discrète sauf à utiliser des maillages appropriés, ce qui n’est pas possible actuellement avec Déform2D.
3.1. Influence de l’orientation des fibres sur la rupture
3.1.1. Simulation
L’orientation des fibres a une grande influence sur les caractéristiques mécaniques du composite.
Modèle du bobinage à 45°. Model of 45° winding.
A gauche, on voit le renfort, en noir, simulant un bobinage croisé à 45° . Les dessins de droite montrent la répartition de la contrainte de traction verticale avant et après fissuration. Les contraintes dans le renfort (couleur plus foncée, figure 4) sont plus importantes que dans la matrice. Certaines zones sont en compression (ici en gris clair). Les mailles fissurées apparaissent entourées d’un trait continu. Seule la matrice est fissurée. Lorsque les fibres sont orientées à 45°, les premières fissures apparaissent tôt, mais la rupture est progressive (figure 5 au milieu).
 Répartition des contraintes à la rupture. Stress distribution at fracture.
Répartition des contraintes à la rupture. Stress distribution at fracture.
Evolution de la force (composantes Fx et Fy) en traction. Evolution of the applied load (Fx and Fy) in tension.
Les oscillations à droite des courbes sont peut-être d’origine numérique. La résistance en traction, neuf fois plus faible que lorsque les fibres sont verticales est légèrement supérieure à celle de la résine
On obtient évidemment les meilleures
caractéristiques mécaniques lorsque les fibres sont parallèles à
l’effort ( figure 5 en haut). La résistance est alors simplement celle
des fibres, même s’il y a rupture de la matrice.
Lorsque les fibres
sont perpendiculaires à l’effort appliqué (fibres horizontales), il
n’y a plus aucun renforcement du matériau. La résistance en traction,
onze fois plus faible que lorsque les fibres sont verticales, est, à
peu de choses près, celle de la résine.
On remarque en bas de la figure ci-contre des oscillations au début et à la fin de la courbe. Elles correspondent à la réflexion des ondes créées par la discontinuité de vitesse au démarrage et par le choc provoqué par la rupture des fibres. Elles sont plus visibles lorsque les fibres sont perpendiculaires à l’effort. En effet, les fibres doivent être peu nombreuses pour une durée de calcul raisonnable.
3.1.2. Comparaison avec l’expérience
Une étude de l’influence de l’angle de bobinage sur les caractéristiques mécaniques de tubes avait été faite [8]. Les constantes élastiques avaient été comparés avec celles calculées par la théorie de Puck.
En utilisant Déform2D, on doit retrouver ces résultats. On donne sur le tableau les valeurs issues de la simulation et les valeurs expérimentales du module d’élasticité, du coefficient de Poisson et de la résistance en traction.
Tableau: Module d’Young, coefficient de Poisson et résistance en traction, simulation et expérience.
Table : Young’ modulus, Poisson’s ratio and tensile strength, simulation and experiment.

En contraintes planes, on retrouve bien une valeur égale ou légèrement supérieure à 0,5 pour le coefficient de Poisson dans le cas d’un bobinage à 45 °. Les modules à 90 et 0 ° ne sont pas connus expérimentalement, les angles de bobinage minimal et maximal étant respectivement de 15 et 80°. Les valeurs expérimentales du module d’élasticité sont inférieures aux valeurs calculées par le logiciel et aux valeurs calculées par la théorie de Puck, mais restent dans les limites de la dispersion des mesures. Les résultats du calcul en déformations planes sont donnés à titre indicatif.
L’écart sur la résistance mécanique est maximal pour le bobinage à 45° où les valeurs calculées sont de 30% inférieures aux valeurs moyennes expérimentales. L’écart est significatif car la précision sur la contrainte de rupture est meilleure que sur le module. Ceci pourrait s’expliquer par l’inhomogénéité du matériau, qui a une influence sensible sur les mesures de déformation par jauges de «contrainte».
3.2. Délaminage en flexion
Le délaminage est une caractéristique importante des stratifiés qui les rend insensibles à l’effet d’entaille.
3.2.1. Simulation
 Flexion sur éprouvette entaillée.
Flexion sur éprouvette entaillée.
Bending of a notched sample.
Une étude expérimentale a été effectuée [9]. qui a été simulée numériquement figure 6. Les valeurs numériques utilisées sont celles données par les auteurs de cette étude. La vitesse de déplacement est de 10 m/s au lieu de 1 µ/s pour une durée de calcul raisonnable. Le nombre de noeuds est de 3000. Les fibres apparaissent en noir.
3.2.2. Comparaison avec l’expérience
On retrouve la fissure horizontale dans la matrice, en tête de l’entaille, signalée dans [9]. Les bandes de cisaillement n’apparaissent pas sur la figure 6, mais on peut les observer à plus grande vitesse de sollicitation. Il est vraisemblable que l’on pourrait observer simultanément ces deux effets en optimisant les conditions de l’expérience numérique. La force maximale est de 1 kN au lieu de 0,6 kN. Il n’y a pas eu de rupture de fibre dont la résistance, non connue, est donc sans importance ici.
3.3. Choc
 Impact d’un projectile à vitesse initiale de 1 km/s sur une plaque composite. Impact of a projectile at a speed of 1 km/s on a composite plate.
Impact d’un projectile à vitesse initiale de 1 km/s sur une plaque composite. Impact of a projectile at a speed of 1 km/s on a composite plate.
Les matériaux composites sont utilisés pour les blindages et les pare-chocs car ils absorbent l’énergie cinétique grâce à la déformation et à la rupture de la matrice tout en ayant une grande résistance grâce aux fibres. On a simulé le choc d’un impacteur. Le matériau de l’impacteur est celui des fibres car le logiciel ne permet actuellement d’introduire que deux matériaux constitutifs en tout: les fibres et la matrice. La cible est ici constituée de trois fibres verticales.
La figure précédente montre le résultat du choc. La matrice est presque entièrement plastifiée (hachures à 45°). La fibre centrale est rompue (hachures verticales et horizontales) ainsi que l’impacteur, dont la ruine est presque complète. On remarque le front d’onde qui n’a pas eu le temps de traverser entièrement la cible. Il n’a pas été possible de déterminer s’il s’agissait d’une onde de choc.
4. CONCLUSIONS
Certains logiciels utilisent le concept voisin d’éléments multicouches, mais ils n’ont pas poussé la logique jusqu’au bout, c’est-à-dire de construire un composite directement à partir des matériaux composants sans passer par la phase d’homogénéisation. Le matériau composite simulé par la méthode proposée ici ne peut comporter un grand nombre de fibres et est donc beaucoup plus inhomogène que le matériau réel pour des raisons de durée de calcul. Toutefois, comme le procédé de fabrication crée d’autres irrégularités difficiles à prendre en compte, l’optique proposée ici est parfaitement défendable. On a pu montrer que la précision des calculs est comparable à la précision des mesures et des données expérimentales, d’ailleurs souvent incomplètes ou difficiles à trouver. L’utilisation d’un logiciel tel que Déform2D avant expérimentation réelle peut être utile ne serait-ce que pour réaliser un plan d’expériences complet.
BIBLIOGRAPHIE
[1] B. SCHAEFFER, Programme bidimensionnel de simulation numérique du comportement dynamique des milieux continus déformables, Optimisation des structures et CAO, FEMCAD 87, Hermès, Paris, 1987, pp. 186-194.
[2] Y.C. FUNG, Foundations of Solid Mechanics, Prentice-Hall, Englewood Cliffs, 1965.
[3] S.C. HUNTER, Mechanics of Continuous Media, Wiley, New York, 1983.
[4] B. PERSOZ, Introduction à l'étude de la rhéologie, Dunod, Paris,1960.
[5] M. REINER, Rheology, Theory and Applications, EIRICH, FR. Editor, Vol. 1, Academic Press, New York , 1956, p. 9.
[6] C.W. HIRT, Heuristic Stability Theory for Finite-Difference Equations, J. Comp. Phys. 2, 1968, p. 339.
[7] N.P. VINH Tuong, Sur les calculs et les prévisions des constantes viscoélastiques des matériaux composites, AGARD Conf. Proc No. 63 on Composite Materials, AGARD-CP-63-71, 2-3 avril 1971, Paris.
[8] G. PETER, L. GELDREICH , B. SCHAEFFER, Influence of the winding angle on the mechanical properties of glass reinforced epoxy tubes, Filament Winding II, The Plastics Institute, Londres, 1972.
[9] R.K. BORDIA, B.J. DALGLEISH, P.G. CHARALAMBIDES, A.G. EVANS, Cracking and Damage in a Notched Unidirectional Fiber-Reinforced Brittle Matrix Composite, J. Am. Ceram. Soc., Vol. 74, No. 11, 1991, pp. 2776-80.

/https%3A%2F%2Fprofilepics.canalblog.com%2Fprofilepics%2F2%2F5%2F251882.jpg)
/https%3A%2F%2Fstorage.canalblog.com%2F64%2F27%2F292736%2F92462161_o.jpeg)
/https%3A%2F%2Fstorage.canalblog.com%2F23%2F27%2F292736%2F70560294_o.jpg)
/https%3A%2F%2Fstorage.canalblog.com%2F19%2F68%2F292736%2F64938275_o.jpg)
/https%3A%2F%2Fstorage.canalblog.com%2F50%2F84%2F292736%2F52050599_o.jpg)
/https%3A%2F%2Fstorage.canalblog.com%2F10%2F87%2F292736%2F22707813_o.jpg)
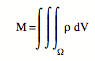





/http%3A%2F%2Fstorage.canalblog.com%2F50%2F80%2F292736%2F25023670_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F40%2F62%2F292736%2F19618255_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F45%2F59%2F292736%2F67702226_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F79%2F05%2F292736%2F73245204_o.jpg)