Paradoxe des jumeaux de Langevin

Langevin avait imaginé un voyage intersidéral de deux ans par un explorateur à l'aide d'un wagon projectile (ou une fusée), capable d'atteindre une vitesse voisine de celle de la lumière, et qu'il allait faire le tour d'un astre situé à une année-lumière de distance. Dans ces conditions, le voyage, pour l'explorateur, aurait duré deux ans, mais la Terre pourrait avoir vieilli de deux cents ans, lorsqu'il serait de retour. C'est ce qu'on appelle maintenant le paradoxe des jumeaux. Il ne semble pas qu'Einstein ait donné son avis sur la question, peut-être pour ne pas gêner Langevin grâce à qui il avait pu présenter sa théorie de la relativité à l'Académie des Sciences. Il n'en a parlé qu'une seule fois en qualifiant cette histoire d'être la chose la plus drôle dont il a pris ses distances "Einstein bezeichnet diese Geschichte als „die drolligste Sache“. Er erwähnt sie später nie wieder. Offensichtlich wollte er sich von ihr distanzieren."

Pour comprendre le paradoxe des jumeaux, la façon la plus simple est de partir de la notion d'espace-temps de la relativité restreinte. D'Alembert, au XVIIe siècle avait déjà imaginé la quatrième dimension, concrétisée par Minkowski et généralisée par Einstein à l'espace courbe pseudo-riemannien. 

Calcul dans l'espace de Minkowski

Considérons d'abord un espace euclidien à deux dimensions, le plan, où se déplacent deux jumeaux J1 et J2 partant de l'origine O des axes Ox et Oy pour atteindre un point P sur l'axe des y. Le premier prend le chemin direct en longeant l'axe des y, l'autre fait un détour pour arriver en P. Le premier aura parcouru la droite Oy sur une distance

et le second sur une courbe de longueur

Lorsqu'ils arrivent en P, ils ont les mêmes coordonnées (0,yP). En posant y=ict, où t est le temps-coordonnée, on passe dans le plan de Minkowski

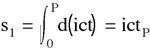
et 

ce qu'on peut écrire en utilisant le temps propre ou intervalle d'espace-temps τ:

et

où v est la vitesse dx/dt du jumeau voyageur par rapport au jumeau casanier. On retrouve la formule donnée par Landau et Lifchitz dans le paragraphe 3 sur le temps propre mais la suite est obscure.

Les deux jumeaux se rejoignent au même point  P de coordonnées (0, ictP) de l'espace-temps et ont donc la même position. Le problème est de savoir si les horloges des jumeaux coïncident ou non lors de leurs retrouvailles.

Géocentrisme

Cependant, le chemin parcouru n'est pas le même. Le jumeau voyageur aura mis moins de temps que le jumeau casanier puisque τ2 est inférieur à τ1. Dans l'espace de MInkowski, un détour est plus court qu'un chemin direct. En réalité le jumeau "immobile" a aussi voyagé, non seulement dans le temps, mais aussi avec la Terre, qui tourne. Il a donc, en plus de la vitesse de la Terre, subi l'accélération de la force centrifuge due à sa rotation et celle due à l'accélération de la pesanteur. Son référentiel n'est donc pas plus galiléen que celui de son jumeau. L'argument qui consiste à dire que le jumeau voyageur n'a pas un mouvement galiléen et que le jumeau casanier en a un ne tient donc pas. Aucun de ces référentiels n'est galiléen aucun n'est privilégié. Il n'y a pas de géocentrisme.

Relativités retreinte et générale

L’accélération centrifuge due à la rotation de la Terre, comme l’accélération de  la gravité, dépend de la direction d’observation. Or l’expérience de Michelson a montré que la vitesse de la lumière était constante et ne dépendait pas de la direction d’observation (ni de la vitesse d'émission comme cela a été montré plus tard grâce à des étoiles de vitesse connue). On pourrait donc en conclure qu'une accélération n'a pas d’influence sur la vitesse de la lumière ni sur l'écoulement du temps selon la relativité restreinte. La relativité générale prévoit pourtant une variation de la vitesse de la lumière dans un champ de gravitation qui ne dépend pas de la direction de l'accélération gravitationnelle. Cela explique donc que la vitesse de la lumière dépend de l'amplitude de la gravitation ou de l'accélération mais pas de sa direction. Dans des référentiels non galiléens on pourrait donc avoir une accélération ou un ralentissement du temps pour un voyage aller-retour mais cela reste à prouver.

L'expérience des mésons

Comme l'a montré l'expérience des mésons, la vitesse a une influence sur leur horloge vue par un observateur terrestre supposé immobile. Il observe une durée de vie des mésons plus grande quand ils se propagent dans la haute atmosphère à une vitesse proche de celle de la lumière qu'en laboratoire où on peut les observer pratiquement au repos. Les mésons, immobiles dans leur référentiel propre, voient les Terriens se propager à grande vitesse et mourir très vite.

L'expérience des horloges embarquées

Les mésons sont observés à distance et ne peuvent être capturés. La situation est différente de celle des jumeaux qui sont réunis au départ et à l'arrivée, ce qui est sans doute impossible à réaliser avec les mésons. On peut le réaliser avec des horloges, ce qui a été fait en leur faisant faire le tour de la Terre en avion. Au retour, lorsque  les horloges se retrouvent au lieu de départ, on constate un faible décalage horaire. Il reste toutefois à prouver par des mesures incontestables que les écarts sont définitifs. En effet, la précision et la signification de l'expérience de Hafele et Keating en 1971 à l'aide d'horloges atomiques embarquées en avion autour de la Terre ont été critiquées par l'inventeur de l'horloge atomique, Louis Essen.

Conclusion

Dans l'état actuel de la science, on ne peut conclure qu'on vieillit moins vite dans un voyage intersidéral qu'en restant dans son lit tournant (donc accéléré) avec la Terre. Il serait donc nécessaire de tenir compte, dans le calcul d`intégration, de la variation de la vitesse, autrement dit, de l`accélération. Des expériences significatives sont encore nécessaires.

Comments

[Bernard Schaeffe]

J’ai oublié de dire qu’il s’agit de l’énergie nucléaire qui serait due à une « force forte »imaginaire,

[Bernard Schaeffe]

J’ai trouvé les2 erreurs des physiciens nucléaires. La première est d’utiliser le dipôle au lieu des charges électriques du proton et du neutron. La deuxième est l’utilisation du magnétisme nucléaire.

[Bernard Schaeffe]

J’ai trouvé les2 erreurs des physiciens nucléaires. La première est d’utiliser le dipôle au lieu des charges électriques du proton et du neutron. La deuxième est l’utilisation du magnétisme nucléaire.

[Mickaël VALLIER]

Pour terminer, et je vais arrêter de discuter ici de choses qui sont assez difficiles à appréhender (maîtriser le langage de la QCD demande du temps, que je n'ai pas), ce que je trouve assez inadmissible, c'est le ton désobligeant que vous employez en affirmant sans aucun argument que tout l'édifice construit qu'on appelle modèle standard est grosso modo une connerie monumentale. Je pense qu'il faut être sacrément gonflé pour affirmer des trucs pareils, alors qu'on ne maîtrise pas soi - même des bases "élémentaires" nécessaires. Autre point, je trouve qu'il faut avoir une certaine estime de soi pour se permettre d'écrire un bouquin qui "clarifie" la relativité et la mécanique quantique alors qu'on ne maîtrise que très "relativement" ces disciplines.



Sur ces mots, qui n'engagent évidemment que moi, je vous laisse dénigrer les lauréats du prix Nobel ainsi que les expérimentateurs qui fabriquent à la pelle des bosons Z (interaction faible) qui n'existent pas !

[Mickaël VALLIER]

Ai-je jamais dit que j'étais "fort" ?

C'est vous qui vous autoproclamez spécialiste des interactions nucléaires !

Le calcul des énergies d'interaction, à partir des connaissances actuelles, est délicat. Je vous ai indiqué des références, vous n'avez pas l'air de vouloir en prendre connaissance...

D'autre part, vous estimez être "le seul" à avoir proposé un modèle ne faisant intervenir que l'interaction électromagnétique : c'est faux (cf Feynman et Speisman).

Un (vieux) papier qui peut vous éclairer :

http://www.iaea.org/inis/collection/NCLCollectionStore/_Public/19/043/19043823.pdf



Mais encore une fois, M.Schaeffer est bien au-dessus de tout ça !



En ce qui me concerne, je ne prétends pas être compétent pour vous sortir une "formule" comme vous dites permettant d'obtenir la valeur de l'énergie d'interaction !